关系数据理论
第六章 关系数据理论
1 理论依据
- 数据依赖:函数依赖、多值依赖、范式(NF)
2 规范化
2.1 理论
规范化理论正是用来改造关系模式,通过分解关系模式来消除其中不合适的数据依赖,以解决插入异常、删除异常、更新异常和数据冗余问题。
2.2 关系模式
由五部分组成,即它是一个五元组:R(U, D, DOM, F)
- R:关系名
- U:组成该关系的属性名集合
- D:属性组U中属性所来自的域
- DOM:属性向域的映象集合
- F:属性间数据的依赖关系集合
简化为一个三元组:R(U, F)
2.3 数据依赖
- 客观世界中事物间的联系:
- 实体与实体的联系——数据模型
- 实体内部属性间的联系——数据依赖
- 属性间的联系分为三类:一对一 、一对多、多对多
- 数据依赖:关系中属性值之间相互依赖相互制约的联系。
- 属性间的数据依赖类型主要有两种:
- 函数依赖
- 多值依赖
2.4 函数依赖
定义:设R(U)是一个属性集U上的关系模式,X和Y是U的子集。若对于R(U)的任意一个可能的关系r,r中不可能存在两个元组在X上的属性值相等, 而在Y上的属性值不等, 则称 “X函数确定Y” 或 “Y函数依赖于X”,记作X→Y。
平凡函数依赖与非平凡函数依赖
- 在关系模式R(U)中,对于U的子集X和Y,
如果X→Y,但Y 包含于 X,则称X→Y是非平凡的函数依赖
若X→Y,但Y 不包含于X, 则称X→Y是平凡的(trivial)函数依赖 - 在关系SC(Sno, Cno, Grade)中,
非平凡函数依赖: (Sno, Cno) → Grade
平凡函数依赖: (Sno, Cno) → Sno (Sno, Cno) → Cno - 若X→Y,则X称为这个函数依赖的决定属性组,也称为决定因素
若X→Y,Y→X,则记作X←→Y。
- 在关系模式R(U)中,对于U的子集X和Y,
完全函数依赖与部分函数依赖
- 定义在R(U)中,如果X→Y,并且对于X的任何一个真子集X’,都有Y不函数依赖于X’, 则称Y对X完全函数依赖,记作
- 若X→Y,但Y不完全函数依赖于X,则称Y对X部分函数依赖,记作
传递函数依赖
属性间的联系决定函数依赖关系
X、Y有1:1关系,则X→Y,Y→X。可表示成:X←→Y。
X、Y有1:m关系,则Y→X,但X不函数依赖于Y。(如班主任:学
生,则学生→班主任,但班主任不函数依赖于学生)
X、Y有n:m关系,则X与Y不存在任何函数依赖。
举例
建立一个描述学生的数据库:
学生的学号(Sno)、所在系(Sdept)、学生住处(Sloc)、课程号(Cno)、成绩(Grade)
单一的关系模式 : Student <U、F>
U ={ Sno, Sdept, Sloc, Cno, Grade }F ={ Sno → Sdept, Sdept → Sloc, (Sno, Cno) → Grade }
Sno → Sdept,Sdept → Sloc Sloc传递函数依赖于Sno
(Sno,Cno)→Grade是完全函数依赖,
(Sno,Cno)→Sdept是部分函数依赖, 因为Sno →Sdept成立,且Sno是(Sno,Cno)的真子集
2.5 码
- 候选码
- 主码
- 主属性和非主属性
- 全码
- 外部码
2.6 范式
各种范式之间存在联系:
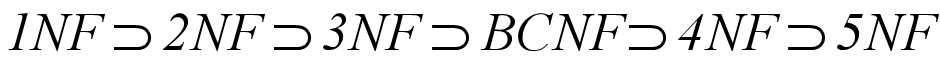
某一关系模式R为第n范式,可简记为R∈nNF。
一个低一级范式的关系模式,通过模式分解可以转换为若干个高一级范式的关系模式的集合,这种过程就叫规范化
2.7 1NF
1NF的定义:如果模一个关系式R的所有属性都是不可分的基本数据项,则R∈1NF
第一范式是对关系模式的最起码的要求。不满足第一范式的数据库模式不能称为关系数据库,但是满足第一范式的关系模式并不一定是一个好的关系模式
- 关系模式 S-L-C(Sno, Sdept, Sloc, Cno, Grade)
- 函数依赖
- S-L-C的码为(Sno, Cno)
S-L-C满足第一范式。
非主属性Sdept和Sloc部分函数依赖于码(Sno, Cno)
2.8 2NF
若R∈1NF,且每一个非主属性完全函数依赖于码,则R∈2NF。
S-L-C(Sno, Cno, Sdept, Sloc, Grade)
插入异常:插入一个学生,还未选课
删除异常:删除一个学生选的唯一课程
数据冗余度大:一个学生选修k门课,Sdept、Sloc重复存储k次
原因:dept、 Sloc部分函数依赖于码。
解决方法:S-L-C分解为两个关系模式,以消除这些部分函数依赖
- 关系模式SC的码为(Sno,Cno)
关系模式S-L的码为Sno
这样非主属性对码都是完全函数依赖
- 关系模式SC的码为(Sno,Cno)
2.9 3NF
若R∈3NF,则每一个非主属性既不部分依赖于码,也不传递依赖于码。
- S-L中存在非主属性对码的传递函数依赖,若一个系换学生宿舍楼,则修改复杂
- 采用投影分解法,把S-L分解为两个关系模式,以消除传递函数依赖,S-D的码为Sno, D-L的码为Sdept。分解后的关系模式S-D与D-L中不再存在传递依赖
2.10 BCNF
每一个决定属性因素都包含码,没有任何属性对码的部分函数依赖和传递函数依赖
若R∈BCNF
所有非主属性对每一个码都是完全函数依赖
所有的主属性对每一个不包含它的码,也是完全函数依赖
没有任何属性完全函数依赖于非码的任何一组属性
在关系模式STJ(S,T,J)中,S表示学生,T表示教师,J表示课程。
- 函数依赖:(S,J)和(S,T)都是候选码
- STJ∈3NF ,没有任何非主属性对码传递依赖或部分依赖
- STJ不属于BCNF,T是决定因素,T不包含码
(S,J)→T
(S,T)→J
T→J
解决方法:将STJ分解为二个关系模式:ST(S,T) ∈ BCNF, TJ(T,J)∈ BCNF
已知一个关系模式的属性之间的语义,也就是相互依赖的关系,如何判断该模式满足第几范式?
- 首先要通过语义把属性之间的函数依赖关系列出来,
- 然后确定哪些属性组合可以候选码,从而找出非主属性和主属性。
- 然后判断是否存在非主属性与码之间的部分函数依赖关系,如果存在,则不满足2NF,如不存在部分函数依赖,则属于2NF,
- 继续进行下一步判断;判断非主属性与码之间存在传递依赖关系,不存在,则为3NF;
- 决定因素是否包含码,满足条件则为BCNF